Quick Start#
Import#
To import mapof-elections python package:
import mapof.elections as mapof
General Tasks#
Generate Ordinal Election from Statistical Culture#
Objective
Generate impartial culture election with 5 candidates and 50 voters.
In this section, you will learn how to generate ordinal elections from different statistical cultures. We will start by defining what we mean by an election.
Formally, an ordinal election is a pair \(E=(C,V)\) that consists of a set of candidates \(C\)
and a collection of voters \(V\), where each voter has a strict preference order (vote),
that is, each voter ranks all the candidates in \(C\) from the most to the least desirable one.
We use terms voter and vote interchangeably.
In practice, we represent an ordinal election by OrdinalElection object, which among other fields, contains:
election.num_candidates # number of candidates
election.num_voters # number of voters
election.votes # preference orders
By votes, we refer to a two-dimensional array, where each row represents a single vote.
Example
E.g., votes = [[0,1,2,3],[2,0,3,1],[3,1,2,0]] refers to an election with three following votes:
0 ≻ 1 ≻ 2 ≻ 3
2 ≻ 0 ≻ 3 ≻ 1
3 ≻ 1 ≻ 2 ≻ 0
To generate an election we use the generate_ordinal_election() function:
election = mapof.generate_ordinal_election(
culture_id='impartial',
num_candidates=5,
num_voters=50)
Generate Approval Election from Statistical Culture#
Objective
Generate impartial culture election with 20 candidates and 100 voters.
In this section, you will learn how to generate approval elections from different statistical cultures. We will start by defining what we mean by an election.
Formally, an approval election is a pair \(E=(C,V)\) that consists of a set of candidates \(C\) and a collection of voters \(V\), where each voter approves a certain subset of candidates. In practice, an ApprovalElection is an object that, among others, contains the following fields:
election.num_candidates # number of candidates
election.num_voters # number of voters
election.votes # list of sets
By votes, we refer to a list of sets, where each set represents a single vote.
Example
For example, votes = [{0,1},{1,2,3},{2}] refers to an election with three following votes:
\({0, 1}\), \({1, 2, 3}\), \({2}\).
To generate an election, we use the generate_approval_election() function:
election = mapof.generate_approval_election(
culture_id='impartial',
num_candidates=20,
num_voters=100)
Generate Ordinal Election from Votes#
Instead of using a statistical culture, you can also generate elections based on your own votes using the generate_ordinal_election_from_votes function.
votes = [[0, 1, 2, 3], [2, 0, 3, 1], [3, 1, 2, 0]]
election = mapof.generate_ordinal_election_from_votes(votes)
Generate Approval Election from Votes#
Instead of using a statistical culture, you can also generate elections based on your own votes using the generate_approval_election_from_votes function.
votes = [{0, 1}, {1, 2, 3}, {2}]
election = mapof.generate_approval_election_from_votes(votes)
Compute Borda Score#
Objective
Compute Borda scores for a given ordinal election.
First, we need to create a scores list and fill it with zeros.
scores = [0 for _ in range(election.num_candidates)]
Second, we need to iterate through all the votes and add appropriate points to candidates.
for vote in election.votes:
for c in range(election.num_candidates):
scores[vote[c]] += election.num_candidates - 1 - c
The complete function looks as follows:
def compute_borda_scores(election) -> list:
""" Returns list with all Borda scores """
scores = [0 for _ in range(election.num_candidates)]
for vote in election.votes:
for c in range(election.num_candidates):
scores[vote[c]] += election.num_candidates - 1 - c
return scores
Compute Distance between Two Elections#
Objective
Compute the EMD-Positionwise distance between two ordinal elections.
To compute a distance, use the compute_distance function, which takes two elections and a distance_id as input.
distances, mapping = mapof.compute_distance(
election_1,
election_2,
distance_id='emd-positionwise')
This function returns a tuple containing the distance and the mapping that witnesses this distance. If a given distance does not use a mapping, it returns None instead.
We start by generating two elections, and then we compute the distance:
election_1 = mapof.generate_ordinal_election(
culture_id='impartial',
num_voters=5,
num_candidates=3)
election_2 = mapof.generate_ordinal_election(
culture_id='impartial',
num_voters=5,
num_candidates=3)
distance, mapping = mapof.compute_distance(
election_1,
election_2,
distance_id='emd-positionwise')
Computing distances between approval elections works in the same way. A list of all implemented distances is available in List of Distances.
Experiments#
Generate Election as Part of Experiment#
Objective
Generate (within experiment) impartial culture election with 5 candidates and 50 voters
In this section, we introduce an abstract object called Experiment, which helps us keep things clear. Finally, we generate elections using the Experiment object.
An Experiment is an abstract object, which, for now, can be seen as a black box in which all the computation takes place. At first, it might be confusing, but in the long run, it simplifies things. Before carrying out any other operations we need to create an empty Experiment. For this, we use the function prepare_online_ordinal_experiment(), which returns an empty Experiment. So, in order to prepare an empty Experiment, type:
experiment = mapof.prepare_online_ordinal_experiment()
To give you a hint of what the Experiment is, we present some of its fields and methods:
experiment.elections
experiment.distances
experiment.coordinates
experiment.features
experiment.add_election()
experiment.add_family()
experiment.compute_distances()
experiment.embed_2d()
experiment.compute_feature()
experiment.print_map_2d()
Now, we will focus on the add_election() method. In order to generate an election, it suffices to run the add_election() method, and specify the culture_id. For example, if we want to generate an election from impartial culture, we type:
experiment.add_election(culture_id='impartial')
All elections added to the experiment are stored in an experiment.elections dictionary, where the key is the election_id, and the value is the Election object. If you want to specify your own election_id, you can do so using the election_id argument, for example:
experiment.add_election(culture_id='impartial', election_id='IC')
By default, the generated election will have 10 candidates and 100 voters. However, if you want to generate an election with a different number of candidates and voters, use the num_candidates and num_voters arguments:
experiment.add_election(culture_id='impartial',
num_candidates=5,
num_voters=50)
If you want to change the default values not for a single election, but for all elections generated in the future, type:
experiment.set_default_num_candidates(5)
experiment.set_default_num_voters(50)
Our aim was to generate an impartial culture election (with 5 candidates and 50 voters) within the experiment. Below we present the code with the solution.
experiment = mapof.prepare_online_ordinal_experiment()
experiment.add_election(culture_id='impartial',
num_candidates=5,
num_voters=50)
Generate Family of Elections#
Objective
Generate 20 elections from Normalized Mallows culture with norm-ϕ = 0.5
If you would like to add many elections from the same culture, instead of adding them one by one, you can add them as one family of elections.
experiment.add_family(culture_id='impartial', size=10)
The main difference between add_election and add_family is the fact that the latter function has an additional argument called size, which specifies how many elections from a given distribution will be created.
Moreover, note that instead of impartial culture, we want to generate Normalized Mallows elections, which are parameterized by norm-ϕ. To generate a single Normalized Mallows election with norm-ϕ = 0.5, we should type:
experiment.add_election(culture_id='norm_mallows', params={'normphi': 0.5})
Joining the upper two things together we obtain the solution.
experiment = mapof.prepare_online_ordinal_experiment()
experiment.add_family(culture_id='norm_mallows', size=10, params={'normphi': 0.5})
You can also specify the name of you family using the ‘family_id’ argument.
experiment.add_family(culture_id='norm_mallows', size=10, params={'normphi': 0.5},
family_id='Norm-Mallows')
Then, the elections will be stored in the experiment.elections dictionary under the keys Norm-Mallows_0, Norm-Mallows_2, … ,``Norm-Mallows_9``.
Create Map of Ordinal Elections#
Objective
Create a map of elections (from impartial and Norm-Mallows cultures).
Creating a map of elections is an ultimate tool of this package. We divide the procedure into four major steps, which we describe in detail one by one, with the exception of the first step which was described before. The steps are the following:
Generate elections
Compute distances
Embed in 2D
Print the map
Compute Distances
In order to compute distances between elections, use the following function:
experiment.compute_distances(distance_id='emd-positionwise')
The distances are stored in the distances field, which is a dictionary of dictionaries. If you want to access the distances, just type:
experiment.distances
Example
Let us assume that we have three elections generated from impartial culture with the following ids: ic_0, ic_1, ic_2. Then, the distances (dictionary of dictionaries) look as follows:
{'ic_0': {'ic_1': 2.3, 'ic_2': 1.7},
'ic_1': {'ic_0': 2.3, 'ic_2': 1.9},
'ic_2': {'ic_0': 1.7, 'ic_1': 1.9}}
Embedding
In order to embed the elections into 2D Euclidean space, run:
experiment.embed_2d(embedding_id='kk')
The coordinates are stored in the coordinates field, which is a dictionary of lists. If you want to access the coordinates, just type:
experiment.coordinates
More information about different embedding algorithms is available in TBU.
Example
Let us assume that we have four elections generated from Normalized Mallows culture with the following ids: mal_0, mal_1, mal_2, mal_3. Then, the coordinates (dictionary of lists) look as follows:
{'mal_1': [0.2, 0.8],
'mal_2': [0.4, 0.4],
'mal_3': [0.3, 0.1],
'mal_4': [0.9, 0.7]}
Printing
In order to print the map, run:
experiment.print_map_2d()

Example 1.#
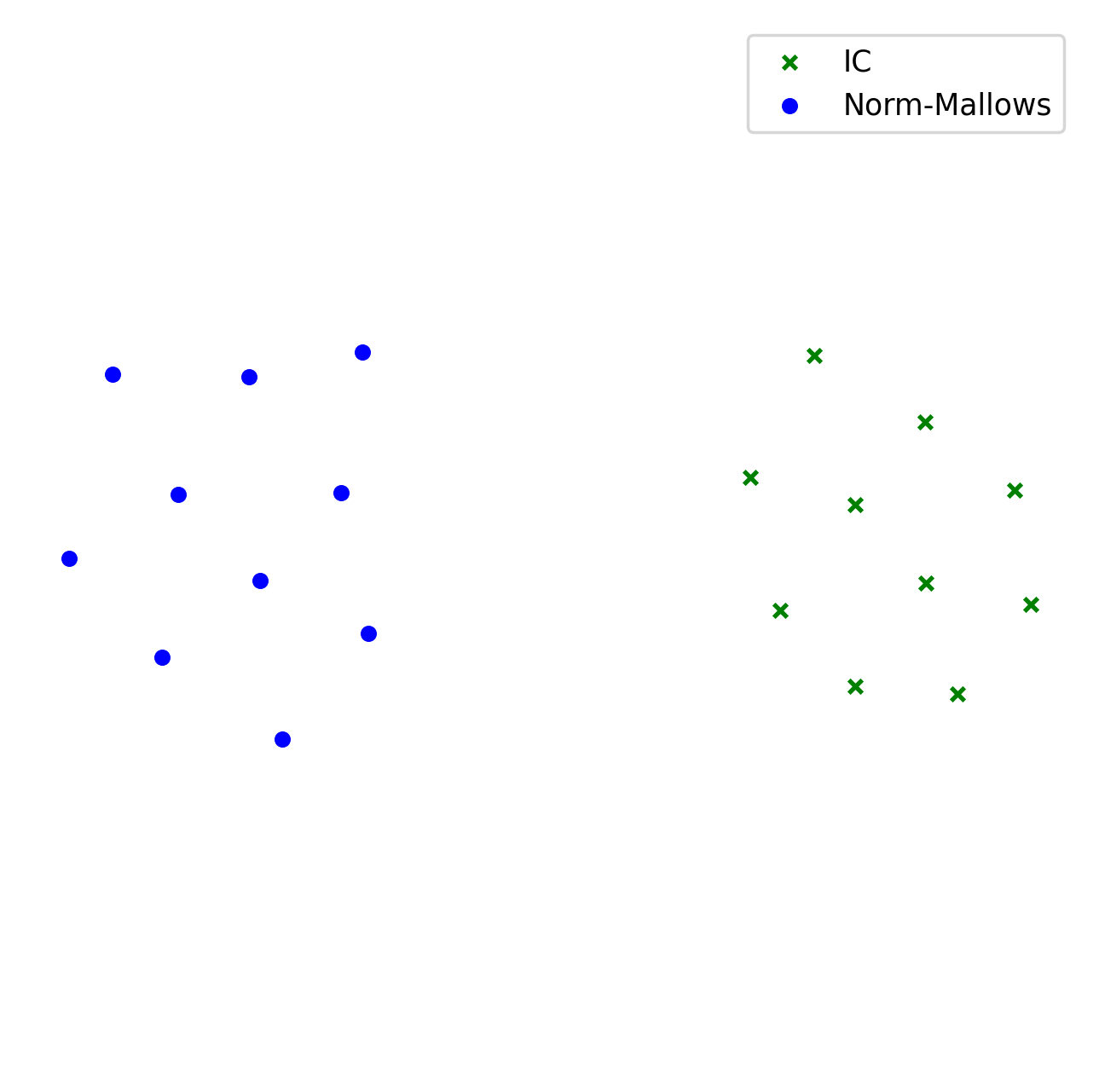
Example 2.#
After combining four steps described above we obtain the following code:
experiment = mapof.prepare_online_ordinal_experiment()
experiment.add_family(culture_id='impartial', size=10)
experiment.add_family(culture_id='norm_mallows', size=10, params={'normphi': 0.5})
experiment.compute_distances(distance_id='emd-positionwise')
experiment.embed_2d(embedding_id='fr')
experiment.print_map_2d()
As a result of the code above, you will see two separate black clouds of points (see Example 1.). In order to make the map more pleasing, we can specify the colors/markers/label of each election or family of elections separately. We do it via color, marker, label arguments.
Improved Solution:
experiment = mapof.prepare_online_ordinal_experiment()
experiment.add_family(culture_id='impartial', size=10,
color='green', marker='x', label='IC')
experiment.add_family(culture_id='norm_mallows', size=10,
params={'normphi': 0.5},
color='blue', marker='o',
label='Norm-Mallows')
experiment.compute_distances(distance_id='emd-positionwise')
experiment.embed_2d(embedding_id='fr')
experiment.print_map_2d()
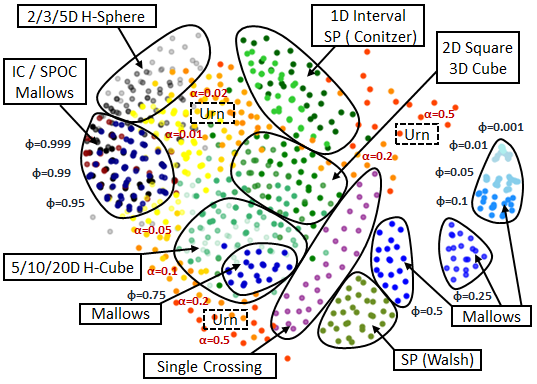
Example 3: A map for the 10x100 dataset of Szufa et al. [2020].#
The picture created by the improved version is presented in Example 2.. Moreover, for illustrative purposes, in Example 3 we present the map for the 10x100 dataset of Szufa et al. [2020]. Note that the labels and arrows are created in PowerPoint and are not part of the mapof software.
Create Map of Approval Elections#
Creating a map of approval elections works similarly to creating a map of ordinal elections. The only differences are the statistical cultures and distances used.
Coloring Map of Elections#
It is interesting to color the map according to certain statistics, referred to as features.
Basic
We offer several pre-implemented features. For example, if you would like to compute the highest plurality score for all elections, you can write:
experiment.compute_feature(feature_id='highest_plurality_score')
To print it, use the feature argument:
experiment.print_map_2d_colored_by_feature(feature_id='highest_plurality_score')
To access the computed values, type:
experiment.features['highest_plurality_score']
List of all the available features can be found in the List of Features.
Printing
Basic arguments for the print_map_2d function are the following:
saveas=str # save file as xyz.png
title=str # title of the image
legend=bool # (by default True) if False then hide the legend
ms=int # (by default 20) size of the marker
show=bool # (by default True) if False then hide the map
cmap # cmap (only for printing features)
For example:
experiment.print_map_2d(title='My First Map', saveas='tmp', ms=30)
Offline Experiment#
Offline experiments are similar to online experiments but offer the possibility to export/import files with elections, distances, coordinates, features, etc.
Prepare Experiment
To prepare an offline experiment, run:
experiment = mapof.prepare_offline_ordinal_experiment(
experiment_id='name_of_the_experiment')
The function above will create the experiment structure as follows:
experiment_id/
├── coordinates/
├── distances/
├── elections/
├── features/
└── map.csv
Prepare Elections
To prepare elections, run:
experiment.prepare_elections()
Elections are generated according to the map.csv file. An example map.csv file is created automatically when preparing the experiment.
All prepared elections are stored in the elections folder in a soc format. The definition of the soc format can be found at Preflib.
map.csv
The controlling map.csv file usually consists of:
size: Number of elections to be generated from a given culture
num_candidates: Number of candidates
num_voters: Number of voters/votes
culture_id: Code of the culture
params: Dictionary with parameters of a given culture
family_id: Family ID
label: Label that will be printed in the legend
color: Color of the point(s) on the map
alpha: Transparency of the point(s)
marker: Marker of the point(s)
ms: Marker size
path: Dictionary with parameters for generating a path of elections
show: If False, the culture will not be displayed on the map
Imports
If some parts of your experiment are already precomputed, you can import them while preparing the experiment. Ensure they are in the proper files. If they were precomputed using mapof, no additional steps are required.
If you want to import specific elements (different from default), specify them while preparing the experiment. For transparency, it is recommended to always define them.
experiment = mapof.prepare_offline_ordinal_experiment(
experiment_id='name_of_the_experiment',
distance_id="emd-positionwise",
embedding_id="kk")
Regarding features, if they are precomputed, the program will import them while printing the map.
Note that, if you will add new elections or families from the code, the map.csv file will be updated automatically.
For example if you will run the following code:
experiment = mapof.prepare_offline_ordinal_experiment(experiment_id='name_of_the_experiment')
experiment.add_family(culture_id='impartial', size=10,
num_candidates=20, num_voters=200,
color='green', marker='s', label='IC')
experiment.add_family(culture_id='urn', size=10,
params={'alpha': 0.1},
num_candidates=20, num_voters=200,
color='blue', marker='o', label='Urn')
The map.csv file will look like this:
size;num_candidates;num_voters;culture_id;params;family_id;label;color;alpha;marker;ms;path;show
10;20;200;impartial;{};impartial_10_100;IC;green;1.0;x;20;{};True
10;20;200;urn;{};urn_10_100;Urn;blue;0.1;o;20;{};True
Other#
Own Cultures
If you want to add your own culture, you can do this by using the add_culture() function.
experiment.add_culture("my_name", my_func)
The function takes two arguments: The first one is the name of the new culture, and the second one is the function that generates the votes. The function that generates the votes can take any number of arguments, but among others, it must take num_candidates and num_voters parameters. Moreover, the function should return a numpy array with votes.
Own Features
If you want to add your own feature, you can do this by using the add_feature() function.
experiment.add_feature("my_name", my_func)
The function takes two arguments: the first is the name of the new feature, and the second is the function that computes that feature. The function that computes the feature can take any number of arguments, but the first must be an election. Moreover, the function should return a dictionary (usually in the format {'value': value}, but it can contain several keys, for example, {'value': value, 'std': std}).
Own Distances
If you want to add your own distance, you can do this by using the add_distance() function.
experiment.add_distance("my_name", my_func)
The function takes two arguments: the first is the name of the new distance, and the second is the function that computes that distance. The function that computes the distance can take any number of arguments, but the first two must be elections. Moreover, the function should return a pair (a float and a list). The first returned value is the distance, and the second is the mapping witnessing that distance; if the distance does not use a mapping, then it should return None instead.
Remark
Functions that store data in files will overwrite the previous data when rerun. For example, if the elections are already created but the command mapof.prepare_elections() is executed again, the old elections will be overwritten. The same is true for other functions such as compute_distances() or embed_2d().
Map of Preferences (aka Microscope)#
A map of preferences is similar to the map of elections; however, now each point represents a single voter (or candidate) instead of representing the whole election.
There are four possible microscopes that one can create: Ordinal-Voters, Ordinal-Candidates, Approval-Voters, and Approval-Candidates. In the following description, we mainly focus on the Ordinal-Voters variant. Given an election, we first have to compute the distances between the votes (compute_distances()). For that, we use the swap distance (optionally the Spearman distance). Next, we perform the embedding (embed()). Finally, we print the microscope (print_map()). For all these functions, we need to set the object_type argument, which can be set to either vote or candidate. Below is the code that generates a microscope from scratch.
election = mapof.generate_ordinal_election(culture_id='norm_mallows',
num_candidates=10,
num_voters=100,
params={'normphi': 0.4})
election.compute_distances(distance_id='swap', object_type='vote')
election.embed(object_type='vote')
election.set_microscope(alpha=0.2, object_type='vote')
election.microscope.show()
Available Distances
Vote Type |
Object Type |
Distances |
|---|---|---|
Ordinal |
vote |
|
Ordinal |
candidate |
|
Approval |
vote |
|
Approval |
candidate |
|
More details about the microscope can be found in the Diversity, Agreement, and Polarization in Elections paper.
Ordinal Compass#
To help us navigate the map, we add four special elections, which we can interpret as compass points.
Identity (ID) – Perfect agreement; all voters have the same preference order.
Uniformity (UN) – Lack of agreement; each candidate takes each position equally often.
Antagonism (AN) – Conflict; half of the voters have opposite preferences to the other half.
4. Stratification (ST) – Partial agreement; voters agree that half of the candidates are better than the other half, but lack agreement on anything else.
Note that, given a number of candidates and a number of voters it is not always possible to create the exact compass elections (especially for UN and ST). In such cases, can either create an approximation of the compass elections or we can directly create a frequency matrix (this is always possible, no matter what is the election size). The latter option is particularly useful if one is planning to use the positionwise distance.
While embedding one can use compass (or any other instances) to help orient the map.
To do so, one can use the left,``up``,``right``,``down`` arguments in the embed_2d() function.
experiment.embed_2d(embedding_id='kk', left='UN', up='AN', right='ID', down='ST')
In the above example, we use the Kamada-Kawai embedding and we use the compass elections to help us orient the map. In practice, it suffice to give only three (out of four) instances to do so. For example, the code below will provide the same outcome as the code below.
experiment.embed_2d(embedding_id='kk', left='UN', up='AN', right='ID')